Kaiming Normal Distribution

Easy:

Imagine you have a magic recipe for making robots smarter. This recipe helps set the starting weights for the robot’s brain so that it can learn quickly and become really good at its tasks. Just like when you start building a tower, you need to place the first blocks carefully to make sure the tower stands tall and strong.

The Kaiming Normal Distribution is like giving the robot the perfect starting blocks. It’s a special way of preparing the robot’s brain so that it can learn fast and solve problems well. By using this special recipe, we make sure the robot’s brain is ready to tackle any challenge and become super smart !

So, think of the Kaiming Normal Distribution as a secret formula that helps robots start off on the right foot, making them clever and efficient in what they do.

Moderate:

The Kaiming Normal Distribution, also known as He Normal Initialization, is a technique used to initialize the weights in neural networks, especially those that employ ReLU (Rectified Linear Unit) activation functions. It was introduced in a 2015 paper by Kaiming He et al.

Here’s the gist of how it works:

• Problem: In deep neural networks, poorly chosen weight initialization can lead to exploding or vanishing gradients during training. This makes it difficult for the network to learn effectively.

• Solution: The Kaiming Normal Distribution addresses this by initializing weights with a specific variance that helps gradients flow properly through the network.

Here’s what makes it special:

• Tailored for ReLU activations: Unlike Xavier initialization (another common technique), which is more general, Kaiming Normal Distribution considers the properties of ReLU activations. This ensures the gradients neither explode nor vanish.

• Specific variance: It uses a normal distribution with a standard deviation of sqrt(2/n), where n is the number of input connections to a neuron. This helps maintain a balanced gradient flow across layers.

Overall, Kaiming Normal Distribution is a valuable tool for initializing weights in neural networks with ReLU activations, promoting smoother training and better performance.

Hard:

“Kaiming Normal Distribution” typically refers to an initialization technique used in neural network training, specifically for the weights of the network. This initialization method is named after Kaiming He, a computer scientist who introduced it in a 2015 paper titled “Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification.”

The Kaiming Normal Initialization is designed to address the challenges associated with initializing the weights of deep neural networks, especially networks that use rectified linear units (ReLUs) as activation functions. ReLUs are popular in deep learning, but they can lead to issues during training if not initialized properly.

In traditional weight initialization methods, such as Gaussian or Xavier (also known as Glorot) initialization, the variance of the weights might diminish or explode as the signal passes through multiple layers of the network. This can lead to vanishing or exploding gradients, making training difficult.

The Kaiming Normal Initialization aims to overcome this problem by adjusting the scale of the weights based on the activation function used. For ReLU activations, the weights are initialized from a Gaussian distribution with mean O(‘Oh’) and a standard deviation calculated using a formula that takes into account the non-linearity introduced by ReLU.

In mathematical terms, if you have a layer with n input units, the weights are initialized from a Gaussian distribution with mean O and standard deviation

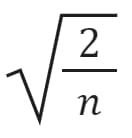
This initialization helps in preventing vanishing or exploding gradients and promotes more stable and efficient training of deep neural networks.

Here’s the formula for Kaiming Normal Initialization: 

where n is the number of input units in the layer.

This initialization technique is commonly used in modern deep learning frameworks and has contributed to the success of training deep neural networks.